Sale
Products at promotional prices, all
Portal Dziecko w Warszawie - banner 755x150
Portal Dziecko w Warszawie - banner 980x150
Portal Dziecko w Warszawie - Artykuł sponsorowany + post FB
Chronos Catalog editon 2024 (e-issue)
Chronos Magazine 1/2024 (e-issue)
Chronos Catalog editon 2019 (e-issue)
Portal Dziecko w Warszawie - banner 1140x150
Chronos Magazine 4-5/2022 (e-issue)
Biblioteka przedsiębiorczych: Wnętrze sklepu (e-issue)
Portal Dziecko w Warszawie - banner 370x200
Biblioteka przedsiębiorczych: Vademecum sprzedawcy (e-issue)
Chronos Magazine 4-5/2024 (e-issue)
Chronos Catalog collection 2020 - 2022
Portal Dziecko w Warszawie - Konkurs sponsorowany
Film&TV Kamera package 2020
Chronos Magazine 2/2024 (e-issue)
Chronos Magazine 1/2023 (e-issue)
Chronos Catalog editon 2018
Chronos Catalog editon 2022 (e-issue)
Chronos Magazine 1/2025 (e-issue)
Chronos Catalog editon 2021
Chronos Magazine 2/2022
Chronos Magazine 2/2025 (e-issue)
Chronos Magazine 2/2023 (e-issue)
Chronos Magazine 4-5/2025 (e-issue)
Chronos Catalog editon 2025 (e-issue)
Film&TV Kamera package 2020
Chronos Catalog collection 2020 - 2021
Chronos Catalog edition 2023 (with a sticker)
Chronos Magazine 4-5/2023 (e-issue)
Chronos Catalog editon 2020
Chronos Catalog editon 2023 (e-issue)
Chronos subscription (e-issues)
Chronos Catalog editon 2021 (e-issue)
Programy
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja wielomianowa liniowa
Pakiet zawiera 13 programów:
-
Kody źródłowe JAVA: Metody numeryczne - Operacje na macierzach
-
Kody źródłowe JAVA: Metody numeryczne - Pierwiastki rzeczywiste wielomianów - metoda stycznych - Newtona
-
Kody źródłowe JAVA: Metody numeryczne - Macierze - obliczanie wyznacznika macierzy stopnia co najmniej piątego i szóstego
-
Kody źródłowe JAVA: Metody numeryczne - Macierze - wybór elementu głównego, wyznacznika, wyniki pośrednie - Metoda Gaussa
-
Kody źródłowe JAVA: Metody numeryczne - Nieliniowe równanie wielomianowe z założoną dokładnością - znajdowanie pierwiastków
-
Kody źródłowe JAVA: Metody numeryczne - Wyznaczniki macierzy - Metoda Gaussa z wyborem elementu głównego w wierszu
-
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja - szukanie wielomianu
-
Kody źródłowe JAVA: Metody numeryczne - Wyznaczanie wielomianu aproksymującego 2. stopnia drugiego dla funkcji dyskretnej
-
Kody źródłowe JAVA: Metody numeryczne - Interpolacja Lagrange\'a
-
Kody źródłowe JAVA: Metody numeryczne - Interpolacja wielomianowa
-
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja wielomianowa - funkcja liniowa i kwadratowa
-
Kody źródłowe JAVA: Metody numeryczne - Współczynnik wielomianu aproksymacyjnego
-
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja wielomianowa liniowa
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja wielomianowa liniowa
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
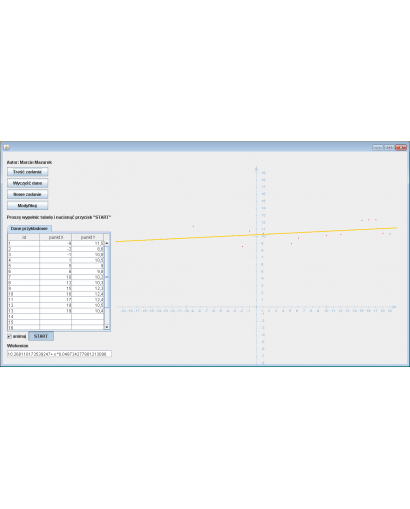
Założenia programu:
Wprowadź punkty szukane i wciśnij przycisk .
Dane przykładowe:
1 -9.0 11.5 2 -2.0 8.6 3 -1.0 10.8 4 1.0 10.5 5 5.0 9.0 6 6.0 9.8 7 10.0 10.2 8 12.0 10.3 9 15.0 12.3 10 16.0 12.4 11 17.0 12.4 12 18.0 10.5 13 19.0 10.4
Wynik:
Wielomian: 10.268110173539247 + x * 0.048734277981213096
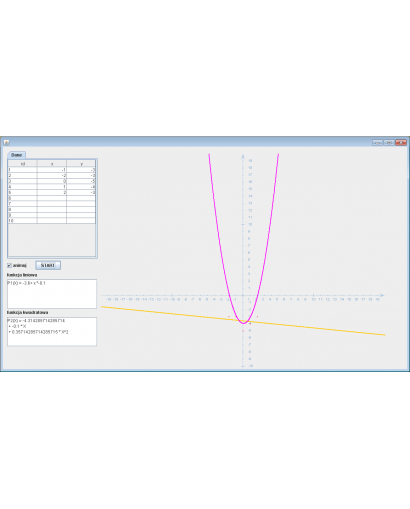
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja wielomianowa - funkcja liniowa i kwadratowa
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Założenia programu:
Wprowadź dane i wciśnij przycisk .
Funkcje aproksymacyjne:
Funkcja liniowa:P1(X) = -3.6 + x * -0.1
Funkcja kwadratowa: P2(X) = -4.314285714285714 + -0.1 * X + 0.35714285714285715 * X^2
Przykładowe dane:
| id | x | y |
|---|---|---|
| 1 | -1.0 | -3.0 |
| 2 | -2.0 | -3.0 |
| 3 | 0.0 | -5.0 |
| 4 | 1.0 | -4.0 |
| 5 | 2.0 | -3.0 |
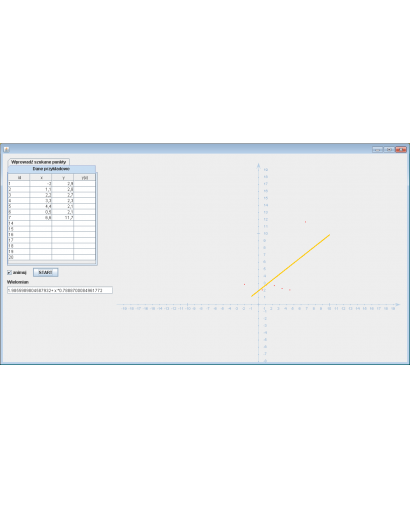
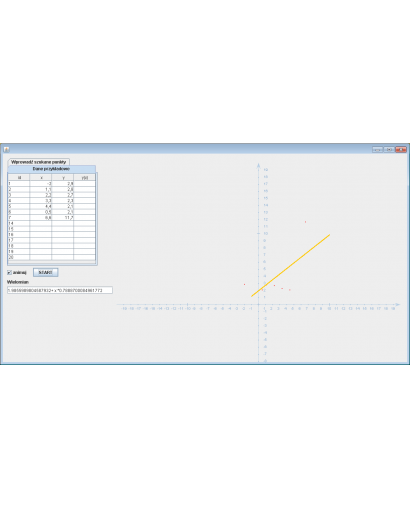
Kody źródłowe JAVA: Metody numeryczne - Aproksymacja - szukanie wielomianu
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
Przykładowe dane:
1 -2.0 2.9
2 1.1 2.8
3 2.2 2.7
4 3.3 2.3
5 4.4 2.1
6 0.5 2.1
7 6.6 11.7
Wynik obliczeń:
Wielomian: 1.9855989804587932 + x * 0.7888700084961772
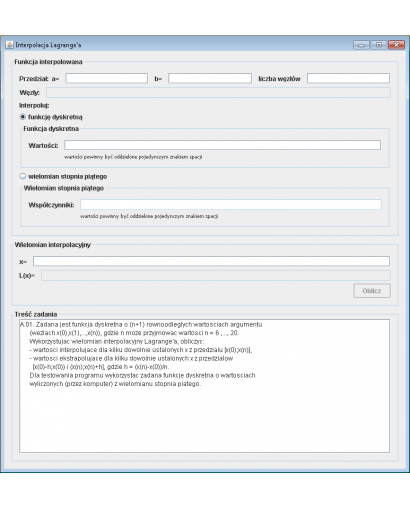
Kody źródłowe JAVA: Metody numeryczne - Interpolacja Lagrange'a
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
Opis produktu
Program służący do interpolacji i ekstrapolacji funkcji dyskretnej przy wykorzystaniu wielomianu interpolacyjnego Lagrange\'a. Zadaniem użytkownika jest dostarczenie zbioru danych (n+1) równoodległych wartości argumentu, gdzie n może przyjmować wartości od 6 do 20.
Możliwości programu
- Obliczanie wartości interpolujących dla dowolnie wybranych punktów x z przedziału [
x(0);x(n)]. - Obliczanie wartości ekstrapolujących dla punktów x z przedziałów [
x(0)-h;x(0)) i (x(n);x(n)+h], gdzieh = (x(n)-x(0))/n.
Testowanie programu
Do testów programu należy wykorzystać zadaną funkcję dyskretną o wartościach wyliczonych z wielomianu stopnia piątego. Wyniki obliczeń umożliwiają weryfikację poprawności implementacji metody Lagrange\'a.
Przykładowe wykorzystanie
// Przykładowy zestaw danych:
x(0) = 0, x(1) = 1, ..., x(6) = 6
// Przykładowe wartości dla funkcji dyskretnej wyliczone z wielomianu stopnia 5:
y(0) = f(x(0)), y(1) = f(x(1)), ..., y(6) = f(x(6))
W celu przeprowadzenia interpolacji lub ekstrapolacji, użytkownik powinien podać żądany punkt x wraz z odpowiednim zestawem danych wejściowych.
Kody źródłowe JAVA: Metody numeryczne - Interpolacja wielomianowa
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
Interpolacja Wielomianowa - przykład giełdowy
Program oblicza wartości interpolowane dla danych giełdowych, wykorzystując metody numeryczne i wielomian interpolacyjny. Program może obliczać dane nie związane z giełdą.
Dane Wejściowe:
Węzeł 1: X=-3.0; Y=10.5
Węzeł 2: X=-2.0; Y=10.6
Węzeł 3: X=-1.0; Y=10.8
Węzeł 4: X=1.0; Y=10.5
Węzeł 5: X=5.0; Y=10.0
Węzeł 6: X=6.0; Y=9.8
Węzeł 7: X=7.0; Y=10.2
Węzeł 8: X=8.0; Y=10.3
Węzeł 9: X=11.0; Y=10.3
Węzeł 10: X=14.0; Y=10.4
Węzeł 11: X=15.0; Y=10.4
Węzeł 12: X=16.0; Y=10.5
Węzeł 13: X=17.0; Y=10.4
Wyniki Interpolacji:
Dzień: 2.03; Wynik: 17.977272727272734
Dzień: 3.03; Wynik: 19.244444444444454
Dzień: 4.03; Wynik: 14.550000000000008
Dzień: 9.03; Wynik: 8.577777777777776
Dzień: 10.03; Wynik: 8.049999999999999
Dzień: 12.03; Wynik: 12.527777777777779
Dzień: 13.03; Wynik: 12.327272727272728
Dzień: 18.03; Wynik: 173.29444444444465
Dzień: 19.03; Wynik: 1488.3999999999996
Dzień: 20.03; Wynik: 7679.35
Wyniki te przedstawiają wartości interpolowane dla wybranych dni, pozwalając przewidywać potencjalne wyniki w dniach, dla których nie posiadamy danych historycznych.
Kody źródłowe JAVA: Metody numeryczne - Wyznaczanie wielomianu aproksymującego 2. stopnia drugiego dla funkcji dyskretnej
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
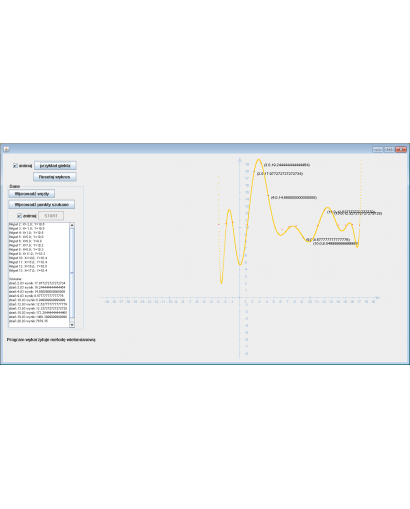
Wyznaczanie wielomianu aproksymującego co najwyżej stopnia drugiego dla funkcji dyskretnej
Program ma za zadanie wyznaczyć wielomian aproksymujący co najwyżej drugiego stopnia dla podanej funkcji dyskretnej. Dodatkowo, program oblicza błąd aproksymacji oraz ilustruje wynik graficznie.
Dane Przykładowe:
1 -9.0 11.5
2 -2.0 8.6
3 -1.0 10.8
4 1.0 10.5
5 5.0 9.0
6 6.0 9.8
7 10.0 10.2
8 12.0 10.3
9 15.0 12.3
10 16.0 12.4
11 17.0 12.4
12 18.0 10.5
13 19.0 10.4
Wynik Aproksymacji:
Wielomian aproksymujący: 10.268110173539247 + x * 0.048734277981213096
Na podstawie powyższych danych program wyznaczył wielomian aproksymujący funkcję dyskretną. W celu obliczenia błędu aproksymacji, program porównuje wartości funkcji dyskretnej z wartościami wyznaczonymi przez wielomian w odpowiadających im punktach. Graficzne przedstawienie wyników pozwala na łatwą weryfikację dokładności aproksymacji.
Kody źródłowe JAVA: Metody numeryczne - Współczynnik wielomianu aproksymacyjnego
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
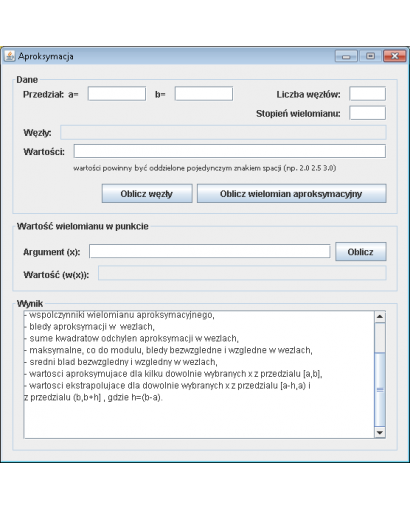
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
W przedziale [a,b] zadana jest funkcja dyskretna dla (n+1) równoodległych wartości argumentu (w węzłach), gdzie n może przyjmować wartości n = 8, ..., 25. Znaleźć wielomian aproksymacyjny ustalonego stopnia s (gdzie s = 1, ..., 6). Obliczyć dla zadanego n i ustalonego s:
- Współczynniki wielomianu aproksymacyjnego,
- Błędy aproksymacji w węzłach,
- Sumę kwadratów odchyleń aproksymacji w węzłach,
- Maksymalne, co do modułu, błędy bezwzględne i względne w węzłach,
- Średni błąd bezwzględny i względny w węzłach,
- Wartości aproksymujące dla kilku dowolnie wybranych
xz przedziału[a,b], - Wartości ekstrapolujące dla dowolnie wybranych
xz przedziału[a-h,a)i z przedziału(b,b+h], gdzieh=(b-a).
Kody źródłowe JAVA: Metody numeryczne - Wyznaczniki macierzy - Metoda Gaussa z wyborem elementu glownego w wierszu
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
[0] Koniec
[1] Wyświetl treść zadania
[2] Oblicz wyznacznik macierzy
Treść zadania:
Metoda Gaussa z wyborem elementu głównego w wierszu obliczyć wyznaczniki dla poniższych macierzy.
Dla jednego z przykładów wyprowadzić wyniki pośrednie.
Przykłady macierzy:
| 0.889 0.774 -0.913 0.398 0.456 0.665 |
| 0.665 0.889 0.774 -0.913 0.398 0.456 |
| 0.456 0.665 0.889 0.774 -0.913 0.398 |
| 0.398 0.456 0.665 0.889 0.774 -0.913 |
| -0.913 0.398 0.456 0.665 0.889 0.774 |
| 0.774 -0.913 0.398 0.456 0.665 0.889 |
--
Przykład działania programu:
Wybierz:
[0] Koniec
[1] Macierz 1
[2] Macierz 2
[3] Macierz 3
[4] Macierz 4
2
Wybrana macierz:
-----------------------------------------------
0.44 1.31 0 0 0 0 0
1.35 -0.86 0 0 0 0 0
0 0 0.34 0.21 1.13 0 0
0 0 0.72 -0.98 0.75 0 0
0 0 0.83 1.27 -0.54 0 0
0 0 0 0 0 0.45 0.18
0 0 0 0 0 0.35 -0.16
-----------------------------------------------
Wyznacznik: -0.01512
Kody źródłowe JAVA: Metody numeryczne - Macierze - wybór elementu głównego, wyznacznika, wyniki pośrednie - Metoda Gaussa
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
[0] Koniec
[1] Wyświetl treść zadania
[2] Oblicz wyznacznik macierzy
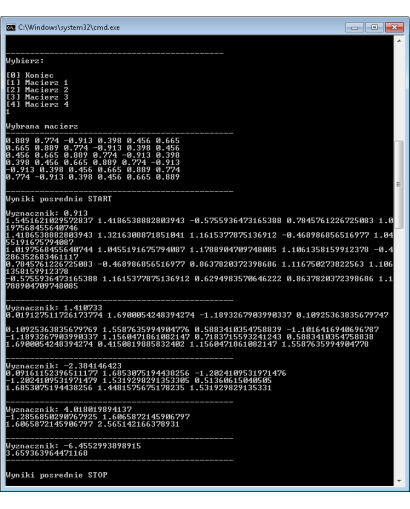
Treść zadania:
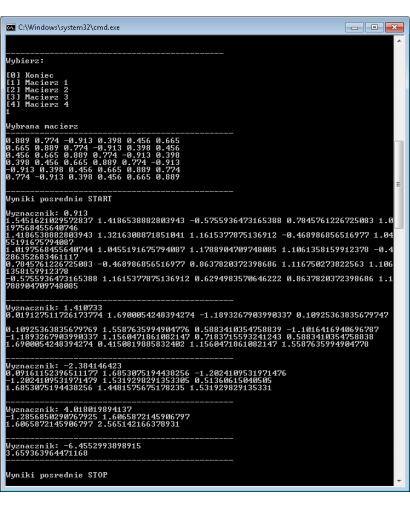
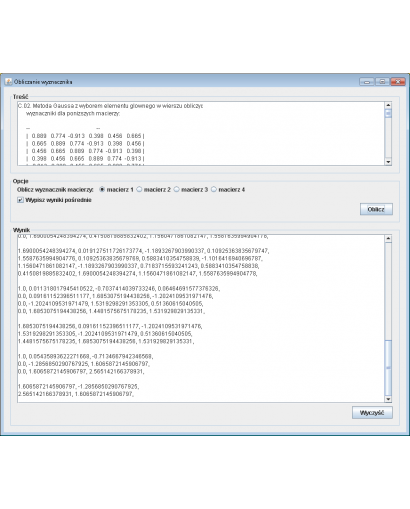
Metoda Gaussa z wyborem elementu głównego w wierszu obliczyć wyznaczniki dla poniższych macierzy:
-- --
| 0.889 0.774 -0.913 0.398 0.456 0.665 |
| 0.665 0.889 0.774 -0.913 0.398 0.456 |
| 0.456 0.665 0.889 0.774 -0.913 0.398 |
| 0.398 0.456 0.665 0.889 0.774 -0.913 |
| -0.913 0.398 0.456 0.665 0.889 0.774 |
| 0.774 -0.913 0.398 0.456 0.665 0.889 |
-- --
Dla jednego z przykładów wyprowadzić wyniki pośrednie.
Obliczam wyznacznik macierzy:
--
--
1.5451621029572837, 1.4186538882803943, -0.5755936473165388, 0.7845761226725083, 1.0197568455640746,
1.4186538882803943, 1.3216308871851041, 1.1615377875136912, -0.468986856516977, 1.0455191675794087,
1.0197568455640744, 1.0455191675794087, 1.1788904709748085, 1.1061358159912378, -0.4286352683461117,
0.7845761226725083, -0.468986856516977, 0.8637820372398686, 1.116750273822563, 1.1061358159912378,
-0.5755936473165388, 1.1615377875136912, 0.6294983570646222, 0.8637820372398686, 1.1788904709748085,
--
--
--
--
--
1.0, -0.8002584717471155,
0.0, 3.659363964471168,
Wyznacznik: -23.62228996724167
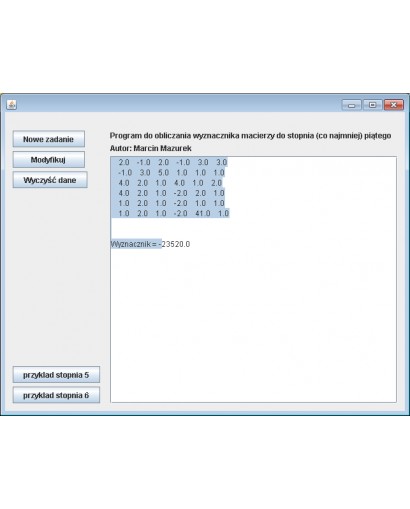
Kody źródłowe JAVA: Metody numeryczne - Macierze - obliczanie wyznacznika macierzy stopnia co najmniej piątego i
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
[0] Koniec
[1] Wyświetl treść zadania
[2] Oblicz wyznacznik macierzy
Treść zadania:
Metoda Gaussa z wyborem elementu głównego w wierszu obliczyć wyznaczniki dla poniższych macierzy:
-- --
| 0.889 0.774 -0.913 0.398 0.456 0.665 |
| 0.665 0.889 0.774 -0.913 0.398 0.456 |
| 0.456 0.665 0.889 0.774 -0.913 0.398 |
| 0.398 0.456 0.665 0.889 0.774 -0.913 |
| -0.913 0.398 0.456 0.665 0.889 0.774 |
| 0.774 -0.913 0.398 0.456 0.665 0.889 |
-- --
Dla jednego z przykładów wyprowadzić wyniki pośrednie.
Obliczam wyznacznik macierzy:
--
--
1.5451621029572837, 1.4186538882803943, -0.5755936473165388, 0.7845761226725083, 1.0197568455640746,
1.4186538882803943, 1.3216308871851041, 1.1615377875136912, -0.468986856516977, 1.0455191675794087,
1.0197568455640744, 1.0455191675794087, 1.1788904709748085, 1.1061358159912378, -0.4286352683461117,
0.7845761226725083, -0.468986856516977, 0.8637820372398686, 1.116750273822563, 1.1061358159912378,
-0.5755936473165388, 1.1615377875136912, 0.6294983570646222, 0.8637820372398686, 1.1788904709748085,
--
--
--
--
--
1.0, -0.8002584717471155,
0.0, 3.659363964471168,
Wyznacznik: -23.62228996724167
Kody źródłowe JAVA: Metody numeryczne - Pierwiastki rzeczywiste wielomi
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
Treść zadania:
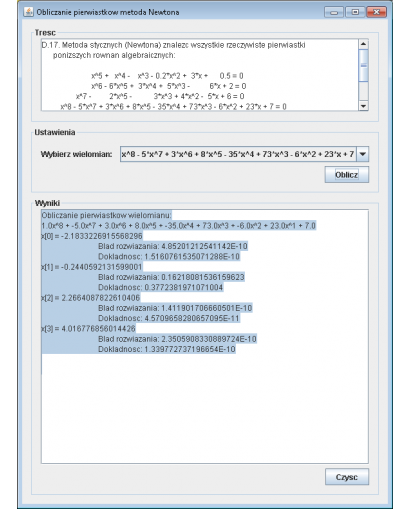
Metoda stycznych (Newtona) znaleźć wszystkie rzeczywiste pierwiastki poniższych równań algebraicznych: x^5 + x^4 - x^3 - 0.2*x^2 + 3*x + 0.5 = 0
x^6 - 6*x^5 + 3*x^4 + 5*x^3 - 6*x + 2 = 0
...
x^9 + 3*x^8 - x^7 + x^6 + 6*x^5 - 7*x^4 + x^3 + x^2 - x + 2 = 0
Podać błędy bezwzględne rozwiązań (|f(x)|) oraz dokładność znalezionych pierwiastków (błąd bezwzględny dwóch ostatnich przybliżeń pierwiastka).
[Pierwiastki rzeczywiste wielomianów - metoda stycznych - Newtona]
Przykładowe rozwiązanie zadania dla wielomianu x^8 - 5*x^7 + 3*x^6 + 8*x^5 - 35*x^4 + 73*x^3 - 6*x^2 + 23*x + 7 = 0:
Obliczanie pierwiastków wielomianu:
1.0x^8 + -5.0x^7 + 3.0x^6 + 8.0x^5 + -35.0x^4 + 73.0x^3 + -6.0x^2 + 23.0x^1 + 7.0
x[0] = -2.1833226915568296
4.85201212541142E-10
Dokładność: 1.5160761535071288E-10
x[1] = -0.2440592131599001
Błąd rozwiązania: 0.16218081536159623
Dokładność: 0.3772381971071004
x[2] = 2.2664087822610406
Błąd rozwiązania: 1.411901706660501E-10
Dokładność: 4.5709658280657095E-11
x[3] = 4.016776856014426
Błąd rozwiązania: 2.3505908330889724E-10
Dokładność: 1.339772737196654E-10
Kody źródłowe JAVA: Metody numeryczne - Nieliniowe równanie wielomianowe z założoną dokładnością - znajdowanie pierwiastów
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
Treść zadania:
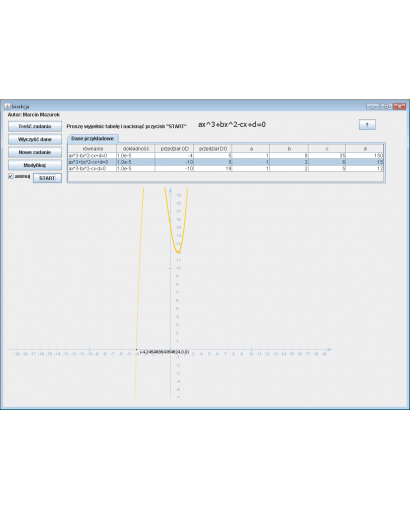
Stworzyć narzędzie do znajdowania we wskazanym przedziale pierwiastków nieliniowego równania wielomianowego z założoną dokładnością. Stworzone narzędzie należy przetestować dla 3 różnych równań, dokonać analizy błędów, a rozwiązanie zilustrować graficznie.
Równanie nr 1: ax^3-bx^2-cx+d=0
Równanie nr 2: ax^3+bx^2-cx+d=0
Równanie nr 3: ax^3-bx^2-cx-d=0
Pole [równanie] - oznacza równanie które zostanie użyte podczas obliczeń
pole [dokładność] - oznacza dokładność obliczeń
pole [przedział OD] - oznacza przedział początkowy
pole [przedział DO] - oznacza przedział końcowy\n" +
pole [a] - oznacza współczynnik \"a\" podstawiany do wybranego równania
pole [b] - oznacza współczynnik \"b\" podstawiany do wybranego równania
pole [c] - oznacza współczynnik \"c\" podstawiany do wybranego równania
pole [d] - oznacza współczynnik \"d\" podstawiany do wybranego równania
Kody źródłowe JAVA: Metody numeryczne - Macierze - wybór elementu głównego, wyznacznika, wyniki pośrednie - Metoda Gaussa
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
Możliwości programu:
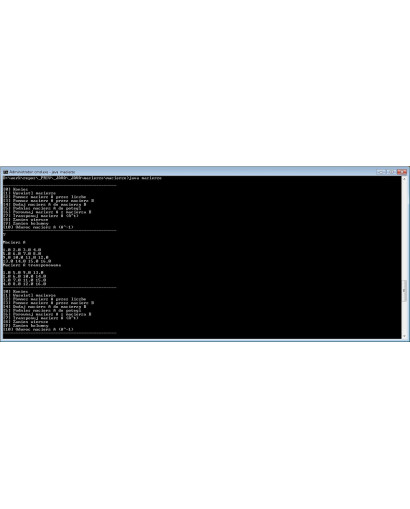
Ten zestaw kodów źródłowych JAVA skupia się na podstawowych i zaawansowanych operacjach numerycznych z wykorzystaniem macierzy.
W pakiecie znajdziesz metody do: mnożenie macierzy, dodawanie macierzy, potęgowanie macierzy, porównywanie macierzy, transpozycja macierzy, odwracanie macierzy.
- Mnożenia macierzy A przez macierz B - algorytm realizujący mnożenie macierzowe zgodnie z regułami algebry.
- Dodawania macierzy A do macierzy B - procedura sumująca odpowiadające sobie elementy obu macierzy.
- Podnoszenia macierzy A do potęgi - metoda obliczająca potęgę macierzy, wykorzystująca szybkie potęgowanie.
- Porównywania macierzy A z macierzą B - funkcja sprawdzająca równość macierzy na podstawie wszystkich elementów.
- Transponowania macierzy A (A^t) - algorytm zamieniający wiersze z kolumnami, tworzący macierz transponowaną.
- Zamiany wierszy - procedura umożliwiająca zmianę kolejności wierszy w macierzy.
- Zamiany kolumn - funkcja pozwalająca na zmianę kolejności kolumn w macierzy.
- Odwracania macierzy A (A^-1) - złożony algorytm obliczający macierz odwrotną, jeżeli istnieje.