Promocje
Produkty w promocyjnych cenach, wszystkie
Chronos Magazyn 4-5/2023 (e-wydanie)
Chronos Katalog edycja 2023 (z naklejką)
Chronos Magazyn 1/2024 (e-wydanie)
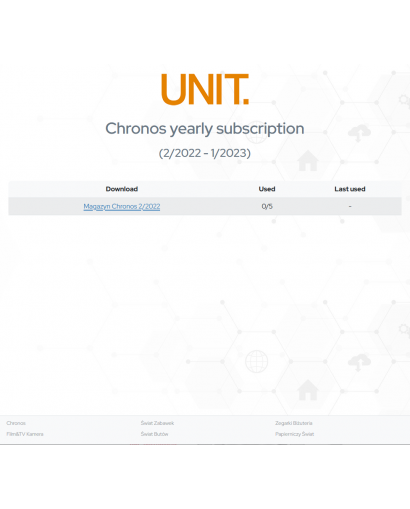
Chronos Magazyn 2/2022
Chronos Katalog edycja 2018
Portal Dziecko w Warszawie - Artykuł sponsorowany + post FB
Chronos Magazyn 1/2025 (e-wydanie)
Chronos Katalog edycja 2022 (e-wydanie)
Chronos Magazyn 4-5/2024 (e-wydanie)
Biblioteka przedsiębiorczych: Vademecum sprzedawcy (e-wydanie)
Chronos Magazyn 2/2024 (e-wydanie)
Chronos Katalog kolekcja 2020 - 2021
Chronos Katalog edycja 2021 (e-wydanie)
Film&TV Kamera pakiet 2020
Chronos Magazyn 4-5/2022 (e-wydanie)
Chronos Magazyn 2/2025 (e-wydanie)
Film&TV Kamera pakiet 2021
Portal Dziecko w Warszawie - banner 1140x150
Chronos Magazyn 2/2023 (e-wydanie)
Chronos Katalog edycja 2023 (e-wydanie)
Chronos prenumerata (e-wydania)
Chronos Katalog edycja 2020
Chronos Magazyn 4-5/2025 (e-wydanie)
Portal Dziecko w Warszawie - banner 755x150
Chronos Katalog edycja 2025 (e-wydanie)
Biblioteka przedsiębiorczych: Wnętrze sklepu (e-wydanie)
Chronos Katalog edycja 2024 (e-wydanie)
Portal Dziecko w Warszawie - Konkurs sponsorowany
Portal Dziecko w Warszawie - Artykuł sponsorowany
Chronos Katalog edycja 2019 (e-wydanie)
Chronos Katalog edycja 2021
Portal Dziecko w Warszawie - banner 980x150
Portal Dziecko w Warszawie - banner 370x200
Chronos Katalog kolekcja 2020 - 2022
Produkty
Biblioteka przedsiębiorczych: Vademecum sprzedawcy (e-wydanie)
Biblioteka przedsiębiorczych: Wnętrze sklepu (e-wydanie)
Chronos Katalog edycja 2015
Chronos Katalog edycja 2016
Chronos Katalog edycja 2017
Chronos Katalog edycja 2018
Chronos Katalog edycja 2019
Chronos Katalog edycja 2019 (e-wydanie)
Chronos Katalog edycja 2020
Chronos Katalog edycja 2021
Chronos Katalog edycja 2021 (e-wydanie)
Chronos Katalog edycja 2022
Chronos Katalog edycja 2022 (e-wydanie)
Chronos Katalog edycja 2023
Chronos Katalog edycja 2023 (e-wydanie)
Chronos Katalog edycja 2023 (z naklejką)
Chronos Katalog edycja 2024
Chronos Katalog edycja 2024 (e-wydanie)
Chronos Katalog edycja 2025
Chronos Katalog edycja 2025 (e-wydanie)
Chronos Katalog edycja 2026
Chronos Katalog edycja 2026 (e-wydanie)
Biblioteka przedsiębiorczych: Franczyza - Twój markowy biznes (e-wydanie)
42 strony, format pliku: PDF
Oddajemy w Państwa ręce publikację biznesową skierowaną do wszystkich zainteresowanych stworzeniem własnej firmy w obszarze franczyzy i dla tych, którzy
już działają na tym polu jako franczyzodawcy. Odpowiadamy w niej m. in. na pytania: Czym jest franczyza? Jakie są jej mocne i słabe strony? Co zawiera umowa, a co pakiet franczyzowy? Jakie są obowiązki franczyzodawcy i franczyzobiorcy? „Franczyza. Twój markowy biznes” to kompendium wiedzy idealne dla wszystkich, którzy chcą prowadzić własny, sprawdzony biznes pod ochronnym parasolem franczyzy.
Joanna Banakiewicz-Brzozowska
Wydanie z roku 2012
Biblioteka przedsiębiorczych: Vademecum sprzedawcy (e-wydanie)
52 strony, format pliku: PDF
VADEMECUM SPRZEDAWCY... czyli co właściciel sklepu wiedzieć. powinien
Od autorki: W tekście niniejszej publikacji przytoczyłam cytaty pochodzące z książki P. Druckera „Zarządzanie w XXI wieku".
Pragnę podziękować redakcji „Mody Forum" i „Świata Zabawek" za pomoc w przygotowaniu i wydaniu tej książki. A dyrektorowi Wydawnictwa UNIT za pouczające i inspirujące dyskusje.
Autor: Anna Bombała.
ISSN: 2084-5758
Wydanie z roku 2012
Biblioteka przedsiębiorczych: Wnętrze sklepu (e-wydanie)
50 stron, format pliku: PDF
Czy wiedzą Państwo, jak zaaranżować przestrzeń sklepu, by sama sprzedawała?
Jak sprawić, by witryna kusiła, światło eksponowało towar, zapach i dźwięk przyciągały klientów? O prezentacji przestrzeni handlowych, ekologicznym visual merchandisingu, budowaniu sklepu z pasją, skutecznej wyprzedaży, aromaiaudiomarketingu oraz innych zagadnieniach przeczytają Państwo w naszej publikacji. „Wnętrze sklepu – stwórz przestrzeń, która sprzedaje” jest skierowane do wszystkich zainteresowanych stworzeniem oraz wzmocnieniem charakteru swojego
sklepu, tak aby… sam sprzedawał.
Życzymy inspirującej lektury!
Redakcja
Wydanie z roku 2012
Bilet wstępu na - Biznes na Plusie, 10-11 czerwca 2026, Warszawa
Cena zawiera:
-
Strefa WIEDZY
-
Strefa BIZNESU
-
Chill Grill
-
Przerwy kawowe
-
Lunch
UWAGA!
Sklepy, hurtownie, sieci, sprzedawcy marketplace (właściciele, kupcy, sprzedawcy)
BEZPŁATNA REJESTRACJA
Więcej szczegółów o wydarzeniu BIZNESNAPLUSIE.pl
Organizatorem wydarzenia jest Wydawnictwo UNIT właściciel marki BIZNESNAPLUSIE.pl - przewaga dzięki wiedzy, magazyn branżowy Zabawki Papier. Książki
Biznes na Plusie - szkolenie. Zmiany prawa w 2026 r.
Rok 2026 przyniesie istotne zmiany w unijnych regulacjach dotyczących bezpieczeństwa produktów, ochrony konsumentów i zrównoważonego rozwoju. Nowe akty prawne – w tym TSR (Toy Safety Regulation), GPSR (General Product Safety Regulation), Paszport Cyfrowy Produktów, a także przepisy dotyczące ROP, mikroplastiku, baterii i CBAM – wprowadzą szereg nowych obowiązków dla firm działających na rynku UE.
Szkolenie w sposób praktyczny omawia, jak przygotować organizację do zmian prawnych w 2026 roku, jakie obowiązki obejmą producentów, importerów i dystrybutorów oraz jak wdrożyć nowe wymogi dotyczące informacji dla konsumentów, dokumentacji i oznakowania produktów.
Prowadząca:
Ilona Skibińska-Mamzer – prawnik, konsultant prawa UE, ekspert w zakresie bezpieczeństwa produktów i compliance, z ponad 14-letnim doświadczeniem w branży zabawek i działalności spółek.
Chronos Katalog edycja 2015
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2015 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2016
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2016 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2017
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2017 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2018
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2018 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2019
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2019 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2020
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2020 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2021
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2021 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2022
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2022 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2023
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2023 (e-wydanie)
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2023 (z naklejką)
Zawiera żółtą naklejkę na głównej okładce.
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2024
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2024 (e-wydanie)
Jedyne pismo tylko o zegarkach
Magazyn Chronos jako jedyne na rynku odczarowuje tajemnice czasu. Odkrywa sekrety największych manufaktur. Prezentuje nowości oraz dokładnie testuje osiągi ekskluzywnych zegarków. Jest swoistą encyklopedią dla miłośników i pasjonatów zegarków, ale również dla tych, którzy zegarkami zajmują się na co dzień. Treści redakcyjne prezentowane na łamach magazynu Chronos uzupełnia portal https://chronosonline.pl.
Chronos Katalog edycja 2025
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2025 (e-wydanie)
Jedyne pismo tylko o zegarkach
Magazyn Chronos jako jedyne na rynku odczarowuje tajemnice czasu. Odkrywa sekrety największych manufaktur. Prezentuje nowości oraz dokładnie testuje osiągi ekskluzywnych zegarków. Jest swoistą encyklopedią dla miłośników i pasjonatów zegarków, ale również dla tych, którzy zegarkami zajmują się na co dzień. Treści redakcyjne prezentowane na łamach magazynu Chronos uzupełnia portal https://chronosonline.pl.
Chronos Katalog edycja 2026
Jedyna na polskim rynku pozycja wydawnicza prezentująca modele zegarków z najnowszych kolekcji prezentowanych na wystawie w Bazylei. Pozycja MUST HAVE dla wszystkich, którzy zegarkami się interesują. Parametry techniczne przy każdym z modeli umożliwiają w łatwy sposób porównywanie i ocenianie zegarków. Ukazuje się raz w roku. Treści redakcyjne prezentowane na łamach katalogu Chronos uzupełnia portal https://chronosonline.pl. Katalog można nabyć oddzielnie, bądź też w ramach prenumeraty Chronos
Chronos Katalog edycja 2026 (e-wydanie)
Jedyne pismo tylko o zegarkach
Magazyn Chronos jako jedyne na rynku odczarowuje tajemnice czasu. Odkrywa sekrety największych manufaktur. Prezentuje nowości oraz dokładnie testuje osiągi ekskluzywnych zegarków. Jest swoistą encyklopedią dla miłośników i pasjonatów zegarków, ale również dla tych, którzy zegarkami zajmują się na co dzień. Treści redakcyjne prezentowane na łamach magazynu Chronos uzupełnia portal https://chronosonline.pl.