Promocje
Produkty w promocyjnych cenach, wszystkie
Chronos Katalog edycja 2024 (e-wydanie)
Portal Dziecko w Warszawie - banner 755x150
Biblioteka przedsiębiorczych: Vademecum sprzedawcy (e-wydanie)
Chronos Katalog edycja 2019 (e-wydanie)
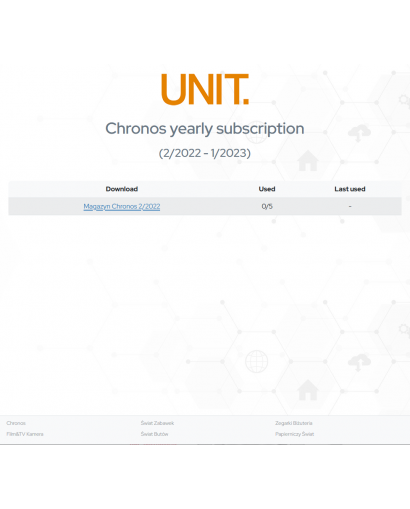
Chronos prenumerata (e-wydania)
Chronos Magazyn 2/2025 (e-wydanie)
Film&TV Kamera pakiet 2021
Chronos Katalog edycja 2021
Chronos Magazyn 1/2023 (e-wydanie)
Chronos Magazyn 2/2022
Biblioteka przedsiębiorczych: Wnętrze sklepu (e-wydanie)
Chronos Katalog kolekcja 2020 - 2022
Chronos Magazyn 4-5/2024 (e-wydanie)
Portal Dziecko w Warszawie - banner 980x150
Chronos Katalog kolekcja 2020 - 2021
Chronos Magazyn 4-5/2025 (e-wydanie)
Chronos Magazyn 2/2024 (e-wydanie)
Film&TV Kamera pakiet 2020
Chronos Katalog edycja 2020
Chronos Magazyn 1/2024 (e-wydanie)
Portal Dziecko w Warszawie - Artykuł sponsorowany
Chronos Katalog edycja 2025 (e-wydanie)
Portal Dziecko w Warszawie - Artykuł sponsorowany + post FB
Chronos Katalog edycja 2018
Chronos Katalog edycja 2023 (z naklejką)
Chronos Magazyn 1/2025 (e-wydanie)
Chronos Katalog edycja 2022 (e-wydanie)
Portal Dziecko w Warszawie - banner 370x200
Chronos Magazyn 2/2023 (e-wydanie)
Chronos Katalog edycja 2021 (e-wydanie)
Chronos Magazyn 4-5/2023 (e-wydanie)
Portal Dziecko w Warszawie - Konkurs sponsorowany
Portal Dziecko w Warszawie - banner 1140x150
Chronos Magazyn 4-5/2022 (e-wydanie)
Wyniki wyszukiwania
Kody źródłowe JAVA: Metody numeryczne - Interpolacja Lagrange'a
Zawartość pakietu:
- Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
- Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
- Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.
Specyfikacja kodu źródłowego:
- Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
- Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.
Instrukcja uruchomienia:
- Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
- Uruchomienie: Użyj pliku
run.batw głównym katalogu programu dla Windows lub wykonajjava -jar nazwa_programu.jarw terminalu. - Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".
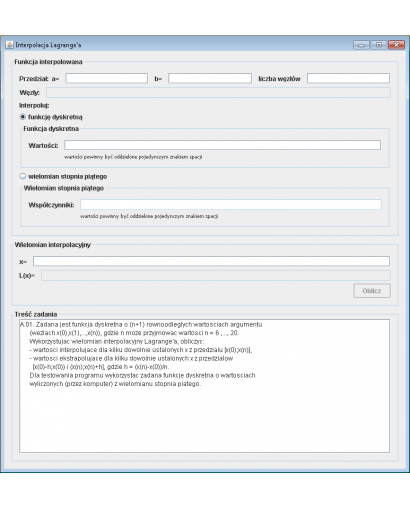
Założenia programu:
Wprowadź dane, a następnie naciśnij przycisk
Opis produktu
Program służący do interpolacji i ekstrapolacji funkcji dyskretnej przy wykorzystaniu wielomianu interpolacyjnego Lagrange\'a. Zadaniem użytkownika jest dostarczenie zbioru danych (n+1) równoodległych wartości argumentu, gdzie n może przyjmować wartości od 6 do 20.
Możliwości programu
- Obliczanie wartości interpolujących dla dowolnie wybranych punktów x z przedziału [
x(0);x(n)]. - Obliczanie wartości ekstrapolujących dla punktów x z przedziałów [
x(0)-h;x(0)) i (x(n);x(n)+h], gdzieh = (x(n)-x(0))/n.
Testowanie programu
Do testów programu należy wykorzystać zadaną funkcję dyskretną o wartościach wyliczonych z wielomianu stopnia piątego. Wyniki obliczeń umożliwiają weryfikację poprawności implementacji metody Lagrange\'a.
Przykładowe wykorzystanie
// Przykładowy zestaw danych:
x(0) = 0, x(1) = 1, ..., x(6) = 6
// Przykładowe wartości dla funkcji dyskretnej wyliczone z wielomianu stopnia 5:
y(0) = f(x(0)), y(1) = f(x(1)), ..., y(6) = f(x(6))
W celu przeprowadzenia interpolacji lub ekstrapolacji, użytkownik powinien podać żądany punkt x wraz z odpowiednim zestawem danych wejściowych.