Zawartość pakietu:

• Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
  • Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
  • Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.

Specyfikacja kodu źródłowego:

• Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
• Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.

Instrukcja uruchomienia:

• Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
• Uruchomienie: Użyj pliku run.bat w głównym katalogu programu dla Windows lub wykonaj java -jar nazwa_programu.jar w terminalu.
• Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".

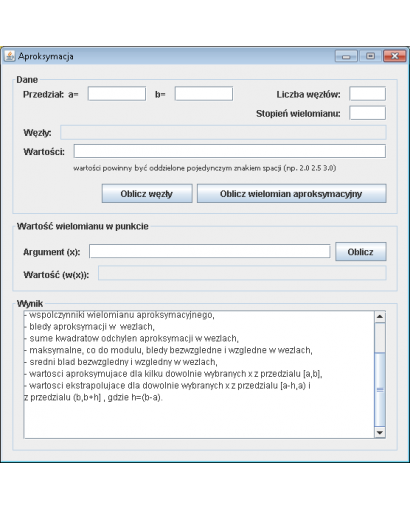
Założenia programu:

Wprowadź dane, a następnie naciśnij przycisk [START]

W przedziale [a,b] zadana jest funkcja dyskretna dla (n+1) równoodległych wartości argumentu (w węzłach), gdzie n może przyjmować wartości n = 8, ..., 25. Znaleźć wielomian aproksymacyjny ustalonego stopnia s (gdzie s = 1, ..., 6). Obliczyć dla zadanego n i ustalonego s:

• Współczynniki wielomianu aproksymacyjnego,
• Błędy aproksymacji w węzłach,
• Sumę kwadratów odchyleń aproksymacji w węzłach,
• Maksymalne, co do modułu, błędy bezwzględne i względne w węzłach,
• Średni błąd bezwzględny i względny w węzłach,
• Wartości aproksymujące dla kilku dowolnie wybranych x z przedziału [a,b],
• Wartości ekstrapolujące dla dowolnie wybranych x z przedziału [a-h,a) i z przedziału (b,b+h], gdzie h=(b-a).

Zawartość pakietu:

• Archiwum ZIP: Zawiera projekt Netbeans i plik JAR.
  • Kody źródłowe: Projekt Netbeans z kodem gotowym do modyfikacji.
  • Executable JAR: Uruchomienie programu w celu szybkiego przetestowania funkcjonalności.

Specyfikacja kodu źródłowego:

• Edytowalność: Kod źródłowy jest dostosowany do szybkich zmian i personalizacji.
• Rozszerzalność: Kod jest konfigurowalny i może być zintegrowany z innymi projektami.

Instrukcja uruchomienia:

• Wymagania: Upewnij się, że Java Runtime Environment (JRE) jest zainstalowana.
• Uruchomienie: Użyj pliku run.bat w głównym katalogu programu dla Windows lub wykonaj java -jar nazwa_programu.jar w terminalu.
• Wsparcie: W przypadku trudności, zapoznaj się z dołączoną instrukcją w sekcji "Jak uruchomić program?".

Założenia programu:

Wprowadź dane, a następnie naciśnij przycisk [START]

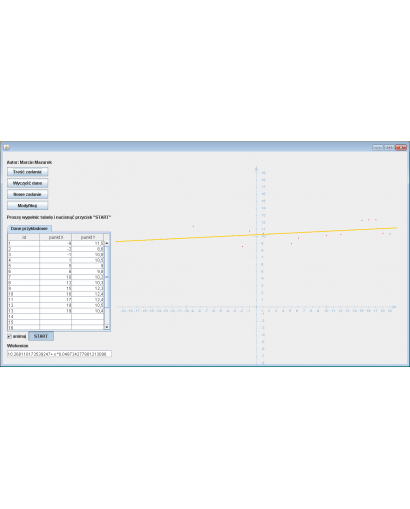
Wyznaczanie wielomianu aproksymującego co najwyżej stopnia drugiego dla funkcji dyskretnej

Program ma za zadanie wyznaczyć wielomian aproksymujący co najwyżej drugiego stopnia dla podanej funkcji dyskretnej. Dodatkowo, program oblicza błąd aproksymacji oraz ilustruje wynik graficznie.

Dane Przykładowe:

1 -9.0 11.5
2 -2.0 8.6
3 -1.0 10.8
4 1.0 10.5
5 5.0 9.0
6 6.0 9.8
7 10.0 10.2
8 12.0 10.3
9 15.0 12.3
10 16.0 12.4
11 17.0 12.4
12 18.0 10.5
13 19.0 10.4


Wynik Aproksymacji:

Wielomian aproksymujący: 10.268110173539247 + x * 0.048734277981213096


Na podstawie powyższych danych program wyznaczył wielomian aproksymujący funkcję dyskretną. W celu obliczenia błędu aproksymacji, program porównuje wartości funkcji dyskretnej z wartościami wyznaczonymi przez wielomian w odpowiadających im punktach. Graficzne przedstawienie wyników pozwala na łatwą weryfikację dokładności aproksymacji.